Single-Photon Avalanche Photodiodes
Achieving the requisite
photocurrent gain for photon flux limited applications often
demands the use of avalanche photodetectors operated in Geiger mode.
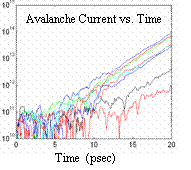 Details of Geiger mode operation, however, pose a number of challenges for
simulation. During each photon detection cycle, the electric field
within the active region of a Geiger mode APD is briefly raised above
the steady-state breakdown value. Electrons and holes photogenerated within the active
region during this time may initiate a series of stochastic impact ionization
events as do subsequent generations of secondary particles, resulting in
a self-perpetuating gain characterized by exponential increase in current
with time, as shown in the first inset.
During this period, electrons and holes in the active region
can gain several eV from the electric field between ionization events,
populating high-lying energy bands and satellite valleys far from their
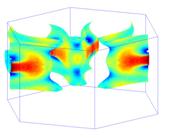
respective band edges. The second inset shows a high-energy surface of
constant energy within the first conduction band of wurtzite GaN. Shading
is proportional to electron group velocity, and is indicative of anisotropy.
Details of Geiger mode operation, however, pose a number of challenges for
simulation. During each photon detection cycle, the electric field
within the active region of a Geiger mode APD is briefly raised above
the steady-state breakdown value. Electrons and holes photogenerated within the active
region during this time may initiate a series of stochastic impact ionization
events as do subsequent generations of secondary particles, resulting in
a self-perpetuating gain characterized by exponential increase in current
with time, as shown in the first inset.
During this period, electrons and holes in the active region
can gain several eV from the electric field between ionization events,
populating high-lying energy bands and satellite valleys far from their
respective band edges. The second inset shows a high-energy surface of
constant energy within the first conduction band of wurtzite GaN. Shading
is proportional to electron group velocity, and is indicative of anisotropy.
Most of the energy gained by charge carriers from the field, however, is lost not to the ionization of valence electrons or conduction holes, but rather to the crystal lattice. This Joule heating leads in turn to a suppression of ionization probability via interactions between charge carriers and a non-equilibrium phonon population. Furthermore, the screening associated with high carrier densities in the active region tends to dynamically redistribute the electric field, likewise suppressing ionization probability. At the end of each photon detection cycle, deliberate reduction of the applied bias ("quenching") initiates the after-pulse recovery cycle, in which charge carriers and lattice temperature relax towards equilibrium. Geiger mode operation must therefore be understood as a non-linear, non-equilibrium, coupled electrothermal problem.
Accurate modeling necessitates going beyond the analytical and semi-numerical treatments of bulk or even non-local avalanche generation, which are restricted to stationary, linear and isothermal applications. In consideration of the aforementioned complications, predictive simulation of Geiger mode APD operation is possible only by full-band ensemble Monte Carlo methods. The Yoder group has over 15 years of experience in this field, and pioneered the technique of self-consistent electrothermal simulation. We investigate the behavior of Geiger mode devices with a wide variety of epitaxial layer structures and device geometries, paying special attention to the role of Joule heating and dynamic screening on the suppression of transient photocurrent gain, and quantify their relationship to parameters such as bias level, optical power, layer thickness and duty cycle. Empirical pseudopotential bandstructure calculations for Wurtzite binary and ternary compound semiconductors provide the electronic dispersion for Monte Carlo simulations.
AlInGaN/InGaN Blue and Green Lasers:
Group III nitrides are in great demand for short wavelength and high power optoelectronic devices. Blue-green light emitting diodes (LEDs) are now commercially available and blue light emission in multiple quantum well (MQW) laser diodes has been demonstrated (Nakamura and Fasol, 1997). These optoelectronic devices involve direct gap materials, exploiting optical transitions at or near the band edges for efficient operation. To model such devices, it is necessary to calculate the electronic dispersion of the underlying materials and determine electronic wavefunctions of complex epitaxial layer structures.
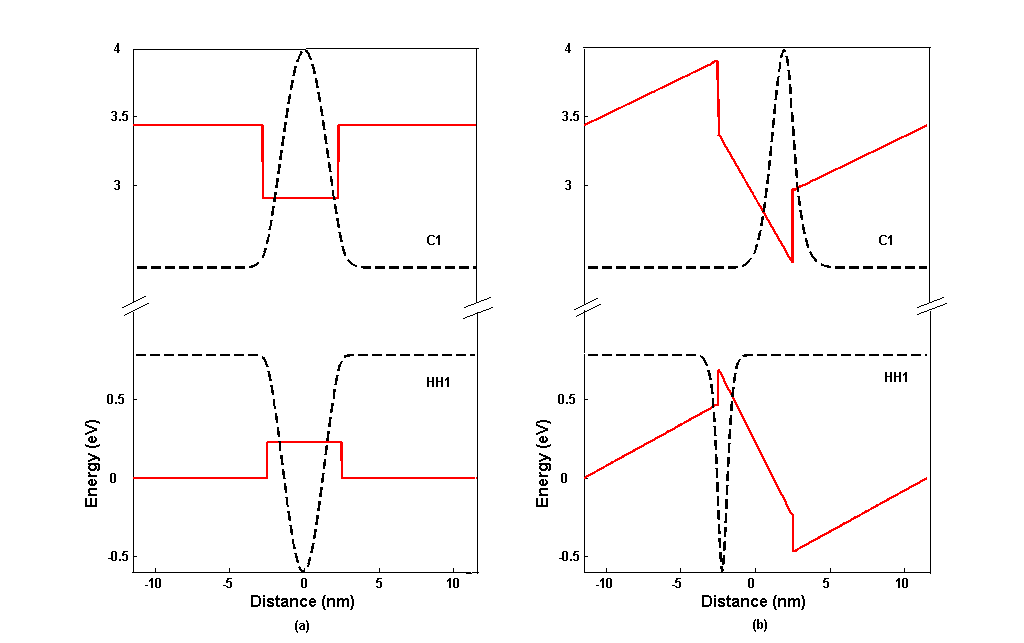
With this aim, we have incorporated models for wurtzite III-V nitride materials into the two-dimensional quantum well laser simulator MINILASE (Song 1990; Grupen 1994, Grupen and Hess 1998). The new simulator, VLS self-consistently solves electronic and optical equations in a quantum well laser. The electronic equations are the Poisson equation and the continuity equations for both free and bound electrons and holes. Charge sources for the Poisson equation are the electron and hole free carrier densities and partially ionized donor and acceptor densities. The continuity equations balance the divergence of the carrier fluxes with the net loss of carrier due to recombination mechanisms like Shockley-Read-Hall and Auger, as well as spontaneous and stimulated radiative recombination. A scalar Helmholtz equation is solved for the optical problem and a photon rate equation is used to calculate the photon spectrum for each mode. Charge transport in the bulk regions is modeled in the drift-diffusion approximation, and ballistic transport across the heterojunctions is treated with Bethe<92>s thermionic emission theory, under the assumption that the heterojunctions are abrupt (Grupen 1994). The electronic band structure of the quantum well is calculated using k.p theory for wurtzite semiconductors (Chuang and Chang 1996). The conduction band is treated according to Loewden's perturbation method and the non-parabolic valence bands are formulated with a 6-band k.p method (Loewden 1951, Chuang and Chang 1996). Many-body e ffects such as band-gap renormalization and Coulomb enhancement of the optical matrix elements are likewise considered, with the former effect included in the local density approximation (Oyafuso et al. 1998). To account for the polar nature of the wurtzite materials, spontaneous and piezoelectric polarization charges have been accounted for in the simulations.
Quasi-unipolar (QU) photodetection:
We have proposed a new concept for high-speed
photodetection, in which unequal numbers of electrons and holes participate
in the photocurrent.
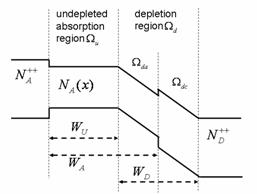 This design strategy offers the advantages of
simultaneously (1) maximizing modulation bandwidth, (2) improving optical
saturation power, and (3) reducing power dissipation. Analytic expressions
are derived for the transport of photogenerated charge, based on a
linearization of the first two moments of the Boltzmann Transport
Equation (BTE).
This design strategy offers the advantages of
simultaneously (1) maximizing modulation bandwidth, (2) improving optical
saturation power, and (3) reducing power dissipation. Analytic expressions
are derived for the transport of photogenerated charge, based on a
linearization of the first two moments of the Boltzmann Transport
Equation (BTE).
Using the method of test functions and a
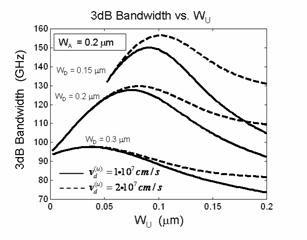 generalization of the Ramo-Shockley theory, microscopic charge and
current densities have been shown to imply an equivalent circuit model
for the QU detector, for which the familiar heterojunction p-i-n (PIN)
and uni-traveling-carrier (UTC) detectors are limiting cases. This
equivalent circuit contrasts substantially with that of the PIN detector
as a result of the nature of charge transport through both depleted and
undepleted material.
generalization of the Ramo-Shockley theory, microscopic charge and
current densities have been shown to imply an equivalent circuit model
for the QU detector, for which the familiar heterojunction p-i-n (PIN)
and uni-traveling-carrier (UTC) detectors are limiting cases. This
equivalent circuit contrasts substantially with that of the PIN detector
as a result of the nature of charge transport through both depleted and
undepleted material.
